In brief:
Some aspects of the Foucault Pendulum which I have not(yet) understood, for which I have not(yet) found a satisfying explanation, for which different sources in the literature give different or sometimes conflicting opinions.
Also, in my data processing I have room for improvement on the subject of fitting a dataset to an ellipse.
I present the problems in the form of study tasks.
The most important theoretical studies I've seen are:
Kamerlingh-Onnes, His thesis (1879, in Dutch. I do not know about an English translation, there seems to exist a German version)
K.O. gives a thourough mathematical description of the behaviour of a point-mass in a rotating co÷rdinate system.
Schumacher, see below.
The biggest problem with Foucault pendulums is the tendency to develop an elliptical path which disturbs the Foucault Precession (FP).
This tendency has nothing to do with the earth's rotation, it would also happen on a stationary planet or on the eart's equator where the FP is absent.
Many publications about ellipse suppression methods exist, but few, if any, report convincing success. With the exception of Charron, who's principle is almost universally used in permanently running pendulums.
Study task:
Explain / derive why an elliptical path develops even in a pendulum on a stationary planet.
Explain / derive why the ellipse problem is more serious in short than in long pendulums.
Or does it only depend on the ratio of length and amplitude?.
Does the Q, the (inverse) amount of energy loss per period, has anything to do with the ellipse forming?
The answers might also be given in the form of a numerical simulation using e.g. finite element methods.
Schumacher derives that when a repelling impulse is given at a certain moment in the pendulum's period that the precession of the ellipse (not the ellipse itself) will be perfectly suppressed.
Study task:
- Check the derivation of Schumacher, make a description of all steps-in-between, such that a less matematically trained person also can follow it.
- Check that the neglections which S. applies are justifyable and acceptable.
- Predict what happens if the impulse is to early or to late, or to strong or to weak, in terms of the FP regularity and total time.
- In my spreadsheet is a section for the Schumacher calculation where manual iteration should be done. Try to automate that iteration process, or better, make it superfluous by making a direct derivation for the correct momernt.
Note: My experiments so far tend to confirm the Schumacher Criterium. Obeying the condition I found that the Foucault Precession was reasonably regular although there was a substantial ellipse which periodically changes direction.
Alternating ellipse:
Kamerlingh-Onnes has mathematically derived the periodical change in ellipse direction, but my knowledge of math is insufficient to follow his derivation.
Study task:
- Explain why the ellipse periodically changes direction using the simplest math.
- Explain why the changes occur when the pendulum swings East-West or North-South.
- Explain / derive if this also would happen on a non-rotating planet.
(solved) - Explain why the amplitude of the short axis varies more like a squarewave than like a sinewave. That is, when it changes it does so quite rapidly, within a few minutes. Is this real or is it an artefact from the way the short amplitude is determined in my software?
Below is a screenshot of the analisys program.
Yellow staircase: time of the day in hours
Cyan: angle of pendulum swing plane, ranging from +180 to - 180 deg. 180 and 0 deg are E-W, +90 and -90 are N-S
White: amplitude of short axis.
Green: Peak amplitude in center detection coil.
The amplitude of the Center coil signal clearly shows maxima when the ellipse changes direction, that is when the bob goes over the center of the system, but no trace of the suddenness of the changes.
2024-01-24: This problem has been solved. The cause was not in the algorithm processing the data, but in the timing of the measured data.
Consider the following: Pendulum period T = 4.16 sec, pendulum amplitude r = 230 mm. So the velocity near the center pass is ϖ.r = 0.347 m/sec.
The information from the Hall sensors is sampled at intervals of ca. 1.5 ms. This corrsponds to a fraction of a mm Bob movement.
The data are sent by the Arduino at a 10 Hz rate, not synchronised with the center pass. So near the center we have information on a 3.47 cm grid.
The info about a CenterPass is sent in the first message after the real pass, in the old situation together with the most recent position info from the Hall sensors. This means when the message with the CenterPass is sent, the Bob may be between 0 and 3.47 cm away from the center, which gives a systematic error in the calculation of the short axis.
The improvement is a small change in the Arduino Firmware, we now freeze the position info at the moment of the center pass, until the message has been sent. The squarewave shape has disappeared now.
Fitting a dataset to an ellipse.
In my dataprocessing I use a rather rude method to derive the ellips parameters (long axis, short axis, angle of long axis and direction) from a set of co-ordinate pairs. See the description here.
There may be a beter way. Something like the least squares fitting of a straigth line
Study task:
Produce an algorithm, preferably written in C or Pascal that:
Given a array of co-ordinate pairs (x, y), laying on the perimeter of an ellipse with some small measurement errors, calculates the long axis, the short axis, the angle of the long axis w.r.t. the horizontal and the direction in which the elliptical path goes.
The long axis of the ellipse can have any direction 0 .. pi. Angles > pi are not distinguishable from angles < pi. The short axis will never be as long as the long axis (circle). The data in the array always start near the center, immediately after a centerpass has been detected, and the data pairs are in the order of the Bob's path.
Crane recommends both attracting and repelling drive with the argument that it would eliminate effects of certain asymmetries in the setup. However he hardly explains which asymmetries these are.
Note that Schumacher has some comment on this.
Study task:
- Give a mathematical derivation that the story about the center magnet is correct/incorrect.
- Indicate what happens when the magnet is to weak/far off or to strong/close by
- Indicate/derive which asymetries can be suppressed by the combination of attracting and repelling drive and indicate what happens if the attracting and repelling impulses are not equal.
Permanent magnet in the center:
Crane recommends a repelling magnet in the center to eliminate the precession of the elipse,
Intuitively it feels that an attracting magnet in the center will reduce the amount of ellipse. After all, when the Bob passes straight over it will not have a net effect, because the effect of the atracting force will be cancelled by that of the repelling force after the pass. However, if there is an ellipse, there will always be an attracting force towards the center.
The contra is: If it is so simple, why is it not done always?
Study task:
- Explain whether or not a permanent magnet in the center of the base unit will reduce the ellipticity. The Bob does have a permanent magnet in the lowest central position.
- Explain what will happen when the magnet is to strong or to weak or is not very precise in the center.
Szostak recommends a repelling drive to counteract the forming of an ellipse. T.m.h.o. his figure 3 indicates just the opposite (Or I do not understand it)
Study task:
- Explain that Sz is right / wrong with his argument in favour of repelling drive.
Make the pendulum swing time independent of the amplitude.
It is known that the period of a pendulum depends slightly on the amplitude, even for very small amplitudes.
With my backgound as electronic engineer i am familiar with the figures of Lissajous, a.o. an ellipse, if you plot two sine shaped signals of the same frequency on an X-Y oscilloscope. The shape and orientation of the ellipse depend on the amplitude and phase of the two signals. If they have exacly the same frequency the ellipse will be stable. If the frequency of the signals differs slightly the ellipse will change shape and orientation in a regular way.
My feeling is that the precession of the Foucault Pendulum's ellipse is connected to the difference in swingtime between the long and short axis' of the ellipse. The Lissajous story tells me that the ellipse should be stable when the swing times are exactly equal
Christian Huygens made the period of his pendulum clocks nearly independent of the amplitude by clamping the top of the "wire" between two cycloidally shaped brackets. The cyclo´d is known to have this property for a pendulum with a specific length.
A picture from Huygens. Upper right the cycloidal brackets.
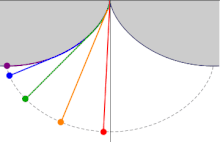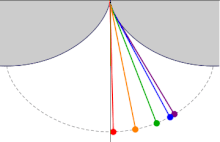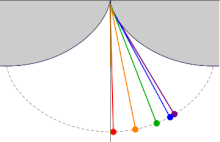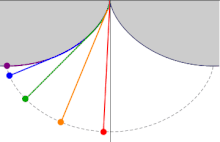
This picture demonstrates that a pendulum with the wire locked between two cycloids has a period independent of the amplitude.
The length of the pendulum must be such that the bob touches the cycloid exactly in the middle.
The question is: If we make the swing time of our pendulum independent of the amplitude, will the ellipse precession disapear?
The Huiygens trick can be applied using a properly shaped tube around the pivoting point (kind of trumpet shape).
The contra is that the formula for the ellipse precession tells me that the precession increases with a larger short-axis. This is contray to the thought where the difference between the short- and long axis' swingtimes is responsible for the precession. In that case we should see less precession when the swingtimes are closer to each other.
Study task:
Pull me out of this swamp.
Pivotting point not well defined.
In my setup there is no well defined pivotting point; the pendulum wire with a finite thickness is mounted in a minature type of drill clamp which is fixed to the structure of my house. The swinging of the pendulum bends the wire slightly making the exact pivotting point go slightly up and down during the swing.
Also bending the wire produces some sideways force on the wire.
Study task:
Given the parameters of the pendulum make an estimate of the way the effective pivotting point moves during the swing, and what the effects might be.
The parameters are: L= 4202 mm, a= 230mm, Bob weight = 5.858 kg, wire thickness 1 mm round, elasticity modulus 210 N/mm▓.
The wire is operated in the range of forces where pure elastic stretching occurs.
Asymmetries in the system:
At many locations an asymmetric situation will exist. Maybe small but certainly not zero. Some known or very likely abberations are:
- The magnet in the bob (or its field) does not sit perfectly in line with the suspension wire and the center-of-mass. This can be seen when the bob is rotating along its own axis. Such a rotation generally occurs when te bob is launched by hand. We can then see that the center-pass time varies slightly with a period of some tens of seconds. Eventually this rotation dies out.
- The drive coil is not perfectly centered w.r.t. the centerpas detection coil. The centerpass coil is rather well centered during the center-adjust procedure, but the drive coil will have some deviation. Also these coils are "wild" wound which may lead to a non-coaxial magnetic field.
- The Rim coil might not be perfectly symmetric around the center- and drive coils.
- The plane in wich the coils lay might not be exacly horizontal.
- The bob has a rather strong magnet and will be influenced by the earth's magnetic field. Also the magnet in the top mount experiences this field.
- Some 30 cm below the coil plane are iron rods as reinforcement in the concrete floor of my living.
Study task:
Give estimations for the effect of these asymmetries.